Các dạng Toán ôn thi vào lớp 10
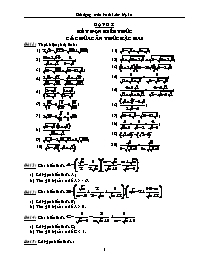
Bài 2: Cho biểu thức
a) Rút gọn biểu thức A;
b) Tìm giá trị của x để A > - 6.
Bài 3: Cho biểu thức
a) Rút gọn biểu thức B;
b) Tìm giá trị của x để A > 0.
Bạn đang xem 20 trang mẫu của tài liệu "Các dạng Toán ôn thi vào lớp 10", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Dạng I: rút gọn biểu thức Có chứa căn thức bậc hai Bài 1: Thực hiện phép tính: 1) ; 2) ; 3) ; 4) ; 5) ; 6) ; 7) ; 8) 9) ; 10) ; 11) ; 12) ; 13) ; 14) ; 15) ; 16) ; 17) ; 18) ; 19) 20) . Bài 2: Cho biểu thức Rút gọn biểu thức A; Tìm giá trị của x để A > - 6. Bài 3: Cho biểu thức Rút gọn biểu thức B; Tìm giá trị của x để A > 0. Bài 4: Cho biểu thức Rút gọn biểu thức C; Tìm giá trị của x để C < 1. Bài 5: Rút gọn biểu thức : a) ; b) ; c) ; d) Bài 6: Cho biểu thức Rút gọn biểu thức M; So sánh M với 1. Bài 7: Cho các biểu thức và Rút gọn biểu thức P và Q; Tìm giá trị của x để P = Q. Bài 8: Cho biểu thức Rút gọn biểu thức P So sánh P với 5. Với mọi giá trị của x làm P có nghĩa, chứng minh biểu thức chỉ nhận đúng một giá trị nguyên. Bài 9: Cho biểu thức Tìm điều kiện để P có nghĩa, rút gọn biểu thức P; Tìm các số tự nhiên x để là số tự nhiên; Tính giá trị của P với x = 4 – 2. Bài 10: Cho biểu thức : Rút gọn biểu thức P; Tìm x để . Dạng II CÁC BÀI TOÁN VỀ HÀM SỐ VÀ ĐỒ THỊ I.Điểm thuộc đường – đường đi qua điểm. Điểm A(xA; yA) thuộc đồ thị hàm số y = f(x) ⟺ yA = f(xA). Vớ dụ 1: Tỡm hệ số a của hàm số: y = ax2 biết đồ thị hàm số của nú đi qua điểm A(2;4). Giải: Do đồ thị hàm số đi qua điểm A(2;4) nờn: 4= a.22 ⟺ a = 1 Vớ dụ 2: Trong mặt phẳng tọa độ cho A(-2;2) và đường thẳng (d) cú phương trỡnh: y = -2(x + 1). Đường thẳng (d) cú đi qua A khụng? Giải: Ta thấy -2.(-2 + 1) = 2 nờn điểm A thuộc v ào đường thẳng (d) II.Cỏch tỡm giao điểm của hai đường y = f(x) và y = g(x). Bước 1: Tỡm hoành độ giao điểm là nghiệm của phương trỡnh f(x) = g(x) (II) Bước 2: Lấy nghiệm đú thay vào 1 trong hai cụng thức y = f(x) hoặc y = g(x) để tỡm tung độ giao điểm. Chỳ ý: Số nghiệm của phương trỡnh (II) là số giao điểm của hai đường trờn. III.Quan hệ giữa hai đường thẳng. Xột hai đường thẳng : (d1) : y = a1x + b1. (d2) : y = a2x + b2. (d1) cắt (d2) ⟺ a1 ≠ a2. d1) // (d2) ⟺ a1=a2b1≠b2 d1) ≡ (d2) ⟺ a1=a2b1=b2 (d1) ⊥ (d2) ⟺ a1 .a2 = -1 IV.Tỡm điều kiện để 3 đường thẳng đồng qui. Bước 1: Giải hệ phương trỡnh gồm hai đường thẳng khụng chứa tham số để tỡm (x;y). Bước 2: Thay (x;y) vừa tỡm được vào phương trỡnh cũn lại để tỡm ra tham số . V.Quan hệ giữa (d): y = ax + b và (P): y = cx2 (c≠0). 1.Tỡm tọa độ giao điểm của (d) và (P). Bước 1: Tỡm hoành độ giao điểm là nghiệm của phương trỡnh: cx2= ax + b (V) Bước 2: Lấy nghiệm đú thay vào 1 trong hai cụng thức y = ax +b hoặc y = cx2 để tỡm tung độ giao điểm. Chỳ ý: Số nghiệm của phương trỡnh (V) là số giao điểm của (d) và (P). 2.Tỡm điều kiện để (d) và (P). a) (d) và (P) cắt nhau ⟺ phương trỡnh (V) cú hai nghiệm phõn biệt. b) (d) và (P) tiếp xỳc với nhau ⟺ phương trỡnh (V) cú nghiệm kộp. c) (d) và (P) khụng giao nhau ⟺ phương trỡnh (V) vụ nghiệm . VI.Viết phương trỡnh đường thẳng y = ax + b biết. 1.Quan hệ về hệ số gúc và đi qua điểm A(x0;y0) Bước 1: Dựa vào quan hệ song song hay vuụng gúc tỡm hệ số a. Bước 2: Thay a vừa tỡm được và x0;y0 vào cụng thức y = ax + b để tỡm b. 2.Biết đồ thị hàm số đi qua điểm A(x1;y1) và B(x2;y2). Do đồ thị hàm số đi qua điểm A(x1;y1) và B(x2;y2) nờn ta cú hệ phương trỡnh: ax1+b=y1ax2+ b=y2 Giải hệ phương trỡnh tỡm a,b. 3.Biết đồ thị hàm số đi qua điểm A(x0;y0) và tiếp xỳc với (P): y = cx2 (c≠0). +) Do đường thẳng đi qua điểm A(x0;y0) nờn cú phương trỡnh : y0 = ax0 + b (3.1) +) Do đồ thị hàm số y = ax + b tiếp xỳc với (P): y = cx 2 (c≠0) nờn: Pt: cx2 = ax + b cú nghiệm kộp ⟺ Δ=0 (3.2) +) Giải hệ gồm hai phương trỡnh trờn để tỡm a,b. VII.Chứng minh đường thẳng luụn đi qua 1 điểm cố định ( giả sử tham số là m). +) Giả sử A(x0;y0) là điểm cố định mà đường thẳng luụn đi qua với mọi m, thay x0;y0 vào phương trỡnh đường thẳng chuyển về phương trỡnh ẩn m hệ số x0;y0 nghiệm đỳng với mọi m. +) Đồng nhất hệ số của phương trỡnh trờn với 0 giải hệ tỡm ra x0;y0. VIII.Một số ứng dụng của đồ thị hàm số. 1.Ứng dụng vào phương trỡnh. 2.Ứng dụng vào bài toỏn cực trị. bài tập về hàm số. Bài tập 1. cho parabol y= 2x2. (p) a. tìm hoành độ giao điểm của (p) với đường thẳng y= 3x-1. b. tìm toạ độ giao điểm của (p) với đường thẳng y=6x-9/2. c. tìm giá trị của a,b sao cho đường thẳng y=ax+b tiếp xúc với (p) và đi qua A(0;-2). d. tìm phương trình đường thẳng tiếp xúc với (p) tại B(1;2). e. biện luận số giao điểm của (p) với đường thẳng y=2m+1. ( bằng hai phương pháp đồ thị và đại số). f. cho đường thẳng (d): y=mx-2. Tìm m để +(p) không cắt (d). +(p)tiếp xúc với (d). tìm toạ độ điểm tiếp xúc đó? + (p) cắt (d) tại hai điểm phân biệt. +(p) cắt (d). Bài tập 2. cho hàm số (p): y=x2 và hai điểm A(0;1) ; B(1;3). a. viết phương trình đường thẳng AB. tìm toạ độ giao điểm AB với (P) đã cho. b. viết phương trình đường thẳng d song song với AB và tiếp xúc với (P). c. viết phương trình đường thẳng d1 vuông góc với AB và tiếp xúc với (P). d. chứng tỏ rằng qua điểm A chỉ có duy nhất một đường thẳng cắt (P) tại hai điểm phân biệt C,D sao cho CD=2. Bài tập 3. Cho (P): y=x2 và hai đường thẳng a,b có phương trình lần lượt là y= 2x-5 y=2x+m a. chứng tỏ rằng đường thẳng a không cắt (P). b. tìm m để đường thẳng b tiếp xúc với (P), với m tìm được hãy: + Chứng minh các đường thẳng a,b song song với nhau. + tìm toạ độ tiếp điểm A của (P) với b. + lập phương trình đường thẳng (d) đi qua A và có hệ số góc bằng -1/2. tìm toạ độ giao điểm của (a) và (d). Bài tập 4. cho hàm số (P) a. vẽ đồ thị hàm số (P). b. với giá trị nào của m thì đường thẳng y=2x+m (d) cắt đồ thị (P) tại hai điểm phân biệt A,B. khi đó hãy tìm toạ độ hai điểm A và B. c. tính tổng tung độ của các hoành độ giao điểm của (P) và (d) theo m. Bài tập5. cho hàm số y=2x2 (P) và y=3x+m (d) khi m=1, tìm toạ độ các giao điểm của (P) và (d). tính tổng bình phương các hoành độ giao điểm của (P) và (d) theo m. tìm mối quan hệ giữa các hoành độ giao điểm của (P) và (d) độc lập với m. Bài tập 6. cho hàm số y=-x2 (P) và đường thẳng (d) đI qua N(-1;-2) có hệ số góc k. a. chứng minh rằng với mọi giá trị của k thì đường thẳng (d) luôn cắt đồ thị (P) tại hai điểm A,B. tìm k cho A,B nằm về hai phía của trục tung. b. gọi (x1;y1); (x2;y2) là toạ độ của các điểm A,B nói trên, tìm k cho tổng S=x1+y1+x2+y2 đạt giá trị lớn nhất. Bài tập7. cho hàm số y= tìm tập xác định của hàm số. tìm y biết: + x=4 + x=(1- )2 + x=m2-m+1 + x=(m-n)2 các điểm A(16;4) và B(16;-4), điểm nào thuộc đồ thị hàm số, điểm nào không thuộc đồ thị hàm số? tại sao. không vẽ đồ thị hãy tìm hoành độ giao điểm của đồ thị hàm số đã cho với đồ thị hàm số y= x-6 Bài tập 8. cho hàm số y=x2 (P) và y=2mx-m2+4 (d) a.tìm hoành độ của các điểm thuộc (P) biết tung độ của chúng y=(1- )2. b.chứng minh rằng (P) với (d) luôn cắt nhau tại 2 điểm phân biệt. tìm toạ độ giao điểm của chúng. với giá trị nào của m thì tổng các tung độ của chúng đạt giá trị nhỏ nhất. Bài tập 9. cho hàm số y= mx-m+1 (d). chứng tỏ rằng khi m thay đổi thì đường thẳng (d) luôn đI qua điểm cố định. tìm điểm cố định ấy. tìm m để (d) cắt (P) y=x2 tại 2 điểm phân biệt A và B, sao cho AB= . Bài tập 10. trên hệ trục toạ độ Oxy cho các điểm M(2;1); N(5;-1/2) và đường thẳng (d) y=ax+b. tìm a và b để đường thẳng (d) đI qua các điểm M, N. xác định toạ độ giao điểm của đường thẳng MN với các trục Ox, Oy. Bài tập 11. cho hàm số y=x2 (P) và y=3x+m2 (d). chứng minh với bất kỳ giá trị nào của m đường thẳng (d) luôn cắt (P) tại 2 điểm phân biệt. gọi y1, y2 kà các tung độ giao điểm của đường thẳng (d) và (P) tìm m để có biểu thức y1+y2= 11y1.y2 bài tập 12. cho hàm số y=x2 (P). vẽ đồ thị hàm số (P). trên (P) lấy 2 điểm A, B có hoành độ lần lượt là 1 và 3. hãy viết phương trình đường thẳng AB. lập phương trình đường trung trực (d) của đoạn thẳng AB. tìm toạ độ giao điểm của (d) và (P). Bài tập 13.. a. viết phương trình đường thẳng tiếp xúc với (P) y=2x2 tại điểm A(-1;2). b. cho hàm số y=x2 (P) và B(3;0), tìm phương trình thoả mãn điều kiện tiếp xúc với (P) và đi qua B. c. cho (P) y=x2. lập phương trình đường thẳng đi qua A(1;0) và tiếp xúc với (P). d. cho (P) y=x2 . lập phương trình d song song với đường thẳng y=2x và tiếp xúc với (P). e. viết phương trình đường thẳng song song với đường thẳng y=-x+2 và cắt (P) y=x2 tại điểm có hoành độ bằng (-1). f. viết phương trình đường thẳng vuông góc với (d) y=x+1 và cắt (P) y=x2 tại điểm có tung độ bằng 9. Dạng III: Hệ phương trình Baứi 1: : Giải các HPT sau: 1.1. a. b. Giải: a. Dùng PP thế: Vaọy HPT đã cho có nghiệm là: Dùng PP cộng: Vaọy HPT đã cho có nghiệm là: Để giảI loại HPT này ta thường sử dụng PP cộng cho thuận lợi. Vaọy HPT có nghiệm là Đối với HPT ở dạng này ta có thể sử dụng hai cách giảI sau đây: 1.2. + Cách 1: Sử dụng PP cộng. ĐK: . Vaọy HPT có nghiệm là + Cách 2: Sử dụng PP đặt ẩn phụ. ĐK: . Đặt ; . HPT đã cho trở thành: (TMĐK) Vaọy HPT có nghiệm là Lưu ý: - Nhiều em còn thiếu ĐK cho những HPT ở dạng này. - Có thể thử lại nghiệm của HPT vừa giải. Baứi 2: Giaỷi caực heọ phửụng trỡnh sau (baống pp theỏ) 1.1: 1.2. Baứi 3: Giaỷi caực heọ phửụng trỡnh sau (baống pp coọng ủaùi soỏ) 2.1. 2.2. Baứi 4: Giaỷi heọ phửụng trỡnh trong moói trửụứng hụùp sau a) m = -1 b) m = 0 c) m = 1 Baứi 5: a) Xaực ủũnh heọ soỏ avaứb, bieỏt raống heọ phửụng trỡnhcoự nghieọm laứ (1; -2) b) Cuừng hoỷi nhử vaọy neỏu heọ phửụng trỡnh coự nghieọm Baứi 6: Giaỷi heọ phửụng trỡnh sau: Tửứ ủoự suy ra nghieọm cuỷa heọ phửụng trỡnh Baứi 7: Giaỷi caực heọ phửụng trỡnh sau: ; ; ; ; ; ; ; ; ; Bài 8: Cho hệ phương trình Giải hệ khi a=3 ; b=-2 Tìm a;b để hệ có nghiệm là (x;y)=( Bài 9: GiảI các hệ phương trình sau a) b) c) (đk x;y2 ) ; ; ; ; ; ; . ; ; ; ; ; Giải bài toán bằng cách lập hệ phương trình. I, Mục tiêu: * Kiến thức: HS giải được các bài toán thực tế bằng cách lập HPT. * Kĩ năng: - HS được củng cố kĩ năng phân tích tìm lời giải, trình bày lời giải bài toán bằng cách lập HPT. * Thái độ: Rèn tính cẩn thận, chính xác, lô gíc chặt chẽ, rõ ràng. II, Lí thuyết cần nhớ: * Bước 1: + Lập HPT - Chọn ẩn, tìm đơn vị và ĐK cho ẩn. - Biểu diễn mối quan hệ còn lại qua ẩn và các đại lượng đã biết. - Lập HPT. * Bước 2: Giải HPT. * Bước 3: Đối chiếu với ĐK để trả lời. III, Bài tập và hướng dẫn: Bài 1. Hai ô tô cùng khởi hành một lúc từ hai tỉnh A và B cách nhau 160 km, đi ngược chiều ... AEDC là hình vuông) => éCMF = 450 hay éCMB = 450. Ta cũng có éCEB = 450 (vì AEDC là hình vuông); éBKC = 450 (vì ABHK là hình vuông). Như vậy K, E, M cùng nhìn BC dưới một góc bằng 450 nên cùng nằm trên cung chứa góc 450 dựng trên BC => 5 điểm b, k, e, m, c cùng nằm trên một đường tròn. 4. DCBM có éB = 450 ; éM = 450 => éBCM =450 hay MC ^ BC tại C => MC là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC. Bài 24. Cho tam giác nhọn ABC có éB = 450 . Vẽ đường tròn đường kính AC có tâm O, đường tròn này cắt BA và BC tại D và E. Chứng minh AE = EB. Gọi H là giao điểm của CD và AE, Chứng minh rằng đường trung trực của đoạn HE đi qua trung điểm I của BH. Chứng minh OD là tiếp tuyến của đường tròn ngoại tiếp tam giác BDE. Lời giải: 1. éAEC = 900 (nội tiếp chắn nửa đường tròn ) => éAEB = 900 ( vì là hai góc kề bù); Theo giả thiết éABE = 450 => DAEB là tam giác vuông cân tại E => EA = EB. 2. Gọi K là trung điểm của HE (1) ; I là trung điểm của HB => IK là đường trung bình của tam giác HBE => IK // BE mà éAEC = 900 nên BE ^ HE tại E => IK ^ HE tại K (2). Từ (1) và (2) => IK là trung trực của HE . Vậy trung trực của đoạn HE đi qua trung điểm I của BH. 3. theo trên I thuộc trung trực của HE => IE = IH mà I là trung điểm của BH => IE = IB. é ADC = 900 (nội tiếp chắn nửa đường tròn ) => éBDH = 900 (kề bù éADC) => tam giác BDH vuông tại D có DI là trung tuyến (do I là trung điểm của BH) => ID = 1/2 BH hay ID = IB => IE = IB = ID => I là tâm đường tròn ngoại tiếp tam giác BDE bán kính ID. Ta có DODC cân tại O (vì OD và OC là bán kính ) => éD1 = éC1. (3) DIBD cân tại I (vì ID và IB là bán kính ) => éD2 = éB1 . (4) Theo trên ta có CD và AE là hai đường cao của tam giác ABC => H là trực tâm của tam giác ABC => BH cũng là đường cao của tam giác ABC => BH ^ AC tại F => DAEB có éAFB = 900 . Theo trên DADC có éADC = 900 => éB1 = éC1 ( cùng phụ éBAC) (5). Từ (3), (4), (5) =>éD1 = éD2 mà éD2 +éIDH =éBDC = 900=> éD1 +éIDH = 900 = éIDO => OD ^ ID tại D => OD là tiếp tuyến của đường tròn ngoại tiếp tam giác BDE. Bài 25. Cho đường tròn (O), BC là dây bất kì (BC< 2R). Kẻ các tiếp tuyến với đường tròn (O) tại B và C chúng cắt nhau tại A. Trên cung nhỏ BC lấy một điểm M rồi kẻ các đường vuông góc MI, MH, MK xuống các cạnh tương ứng BC, AC, AB. Gọi giao điểm của BM, IK là P; giao điểm của CM, IH là Q. 1. Chứng minh tam giác ABC cân. 2. Các tứ giác BIMK, CIMH nội tiếp . 3. Chứng minh MI2 = MH.MK. 4. Chứng minh PQ ^ MI. Lời giải: 1. Theo tính chất hai tiếp tuyến cắt nhau ta có AB = AC => DABC cân tại A. 2. Theo giả thiết MI ^ BC => éMIB = 900; MK ^ AB => éMKB = 900. => éMIB + éMKB = 1800 mà đây là hai góc đối => tứ giác BIMK nội tiếp * ( Chứng minh tứ giác CIMH nội tiếp tương tự tứ giác BIMK ) 3. Theo trên tứ giác BIMK nội tiếp => éKMI + éKBI = 1800; tứ giác CHMI nội tiếp => éHMI + éHCI = 1800. mà éKBI = éHCI ( vì tam giác ABC cân tại A) => éKMI = éHMI (1). Theo trên tứ giác BIMK nội tiếp => éB1 = éI1 ( nội tiếp cùng chắn cung KM); tứ giác CHMI nội tiếp => éH1 = éC1 ( nội tiếp cùng chắn cung IM). Mà éB1 = éC1 ( = 1/2 sđ ) => éI1 = éH1 (2). Từ (1) và (2) => DMKI DMIH => => MI2 = MH.MK 4. Theo trên ta có éI1 = éC1; cũng chứng minh tương tự ta có éI2 = éB2 mà éC1 + éB2 + éBMC = 1800 => éI1 + éI2 + éBMC = 1800 hay éPIQ + éPMQ = 1800 mà đây là hai góc đối => tứ giác PMQI nội tiếp => éQ1 = éI1 mà éI1 = éC1 => éQ1 = éC1 => PQ // BC ( vì có hai góc đồng vị bằng nhau) . Theo giả thiết MI ^BC nên suy ra IM ^ PQ. Bài 26. Cho đường tròn (O), đường kính AB = 2R. Vẽ dây cung CD ^ AB ở H. Gọi M là điểm chính giữa của cung CB, I là giao điểm của CB và OM. K là giao điểm của AM và CB. Chứng minh : 1. 2. AM là tia phân giác của éCMD. 3. Tứ giác OHCI nội tiếp 4. Chứng minh đường vuông góc kẻ từ M đến AC cũng là tiếp tuyến của đường tròn tại M. Lời giải: 1. Theo giả thiết M là trung điểm của => => éCAM = éBAM (hai góc nội tiếp chắn hai cung bằng nhau) => AK là tia phân giác của góc CAB => ( t/c tia phân giác của tam giác ) 2. (HD) Theo giả thiết CD ^ AB => A là trung điểm của => éCMA = éDMA => MA là tia phân giác của góc CMD. 3. (HD) Theo giả thiết M là trung điểm của => OM ^ BC tại I => éOIC = 900 ; CD ^ AB tại H => éOHC = 900 => éOIC + éOHC = 1800 mà đây là hai góc đối => tứ giác OHCI nội tiếp 4. Kẻ MJ ^ AC ta có MJ // BC ( vì cùng vuông góc với AC). Theo trên OM ^ BC => OM ^ MJ tại J suy ra MJ là tiếp tuyến của đường tròn tại M. Bài 27 Cho đường tròn (O) và một điểm A ở ngoài đường tròn . Các tiếp tuyến với đường tròn (O) kẻ từ A tiếp xúc với đường tròn (O) tại B và C. Gọi M là điểm tuỳ ý trên đường tròn ( M khác B, C), từ M kẻ MH ^ BC, MK ^ CA, MI ^ AB. Chứng minh : Tứ giác ABOC nội tiếp. 2. éBAO = é BCO. 3. DMIH ~ DMHK. 4. MI.MK = MH2. Lời giải: (HS tự giải) Tứ giác ABOC nội tiếp => éBAO = é BCO (nội tiếp cùng chắn cung BO). Theo giả thiết MH ^ BC => éMHC = 900; MK ^ CA => éMKC = 900 => éMHC + éMKC = 1800 mà đây là hai góc đối => tứ giác MHCK nội tiếp => éHCM = éHKM (nội tiếp cùng chắn cung HM). Chứng minh tương tự ta có tứ giác MHBI nội tiếp => éMHI = éMBI (nội tiếp cùng chắn cung IM). Mà éHCM = éMBI ( = 1/2 sđ ) => éHKM = éMHI (1). Chứng minh tương tự ta cũng có éKHM = éHIM (2). Từ (1) và (2) => D HIM ~ D KHM. Theo trên D HIM ~ D KHM => => MI.MK = MH2 Bài 28 Cho tam giác ABC nội tiếp (O). Gọi H là trực tâm của tam giác ABC; E là điểm đối xứng của H qua BC; F là điểm đối xứng của H qua trung điểm I của BC. Chứng minh tứ giác BHCF là hình bình hành. E, F nằm trên đường tròn (O). Chứng minh tứ giác BCFE là hình thang cân. Gọi G là giao điểm của AI và OH. Chứng minh G là trọng tâm của tam giác ABC. Lời giải: 1. Theo giả thiết F là điểm đối xứng của H qua trung điểm I của BC => I là trung điểm BC và HE => BHCF là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường . 2. (HD) Tứ giác AB’HC’ nội tiếp => éBAC + éB’HC’ = 1800 mà éBHC = éB’HC’ (đối đỉnh) => éBAC + éBHC = 1800. Theo trên BHCF là hình bình hành => éBHC = éBFC => éBFC + éBAC = 1800 => Tứ giác ABFC nội tiếp => F thuộc (O). * H và E đối xứng nhau qua BC => DBHC = DBEC (c.c.c) => éBHC = éBEC => é BEC + éBAC = 1800 => ABEC nội tiếp => E thuộc (O) . 3. Ta có H và E đối xứng nhau qua BC => BC ^ HE (1) và IH = IE mà I là trung điểm của của HF => EI = 1/2 HE => tam giác HEF vuông tại E hay FE ^ HE (2) Từ (1) và (2) => EF // BC => BEFC là hình thang. (3) Theo trên E ẻ(O) => éCBE = éCAE ( nội tiếp cùng chắn cung CE) (4). Theo trên F ẻ(O) và éFEA =900 => AF là đường kính của (O) => éACF = 900 => éBCF = éCAE ( vì cùng phụ éACB) (5). Từ (4) và (5) => éBCF = éCBE (6). Từ (3) và (6) => tứ giác BEFC là hình thang cân. 4. Theo trên AF là đường kính của (O) => O là trung điểm của AF; BHCF là hình bình hành => I là trung điểm của HF => OI là đường trung bình của tam giác AHF => OI = 1/ 2 AH. Theo giả thiết I là trung điểm của BC => OI ^ BC ( Quan hệ đường kính và dây cung) => éOIG = éHAG (vì so le trong); lại có éOGI = é HGA (đối đỉnh) => DOGI ~ DHGA => mà OI = AH => mà AI là trung tuyến của tam giác ABC (do I là trung điểm của BC) => G là trọng tâm của tam giác ABC. Bài 29 BC là một dây cung của đường tròn (O; R) (BC 2R). Điểm A di động trên cung lớn BC sao cho O luôn nằm trong tam giác ABC. Các đường cao AD, BE, CF của tam giác ABC đồng quy tại H. Chứng minh tam giác AEF đồng dạng với tam giác ABC. Gọi A’ là trung điểm của BC, Chứng minh AH = 2OA’. Gọi A1 là trung điểm của EF, Chứng minh R.AA1 = AA’. OA’. Chứng minh R(EF + FD + DE) = 2SABC suy ra vị trí của A để tổng EF + FD + DE đạt giá trị lớn nhất. Lời giải: (HD) 1. Tứ giác BFEC nội tiếp => éAEF = éACB (cùng bù éBFE) éAEF = éABC (cùng bù éCEF) => D AEF ~ D ABC. 2. Vẽ đường kính AK => KB // CH ( cùng vuông góc AB); KC // BH (cùng vuông góc AC) => BHKC là hình bình hành => A’ là trung điểm của HK => OK là đường trung bình của DAHK => AH = 2OA’ 3. áp dụng tính chất : nếu hai tam giác đồng dạng thì tỉ số giữa hia trung tuyến, tỉ số giữa hai bán kính các đường tròn ngoại tiếp bằng tỉ số đồng dạng. ta có : D AEF ~ D ABC => (1) trong đó R là bán kính đường tròn ngoại tiếp DABC; R’ là bán kính đường tròn ngoại tiếp D AEF; AA’ là trung tuyến của DABC; AA1 là trung tuyến của DAEF. Tứ giác AEHF nội tiếp đường tròn đường kính AH nên đây cũng là đường tròn ngoại tiếp DAEF Từ (1) => R.AA1 = AA’. R’ = AA’ = AA’ . Vậy R . AA1 = AA’ . A’O (2) 4. Gọi B’, C’lần lượt là trung điểm của AC, AB, ta có OB’^AC ; OC’^AB (bán kính đi qua trung điểm của một dây không qua tâm) => OA’, OB’, OC’ lần lượt là các đường cao của các tam giác OBC, OCA, OAB. SABC = SOBC+ SOCA + SOAB =( OA’ . BC’ + OB’ . AC + OC’ . AB ) 2SABC = OA’ . BC + OB’ . AC’ + OC’ . AB (3) Theo (2) => OA’ = R . mà là tỉ số giữa 2 trung tuyến của hai tam giác đồng dạng AEF và ABC nên = . Tương tự ta có : OB’ = R .; OC’ = R . Thay vào (3) ta được 2SABC = R () ú 2SABC = R(EF + FD + DE) * R(EF + FD + DE) = 2SABC mà R không đổi nên (EF + FD + DE) đạt gí trị lớn nhất khi SABC. Ta có SABC = AD.BC do BC không đổi nên SABC lớn nhất khi AD lớn nhất, mà AD lớn nhất khi A là điểm chính giỡa của cung lớn BC. Bài 30 Cho tam giác ABC nội tiếp (O; R), tia phân giác của góc BAC cắt (O) tại M. Vẽ đường cao AH và bán kính OA. Chứng minh AM là phân giác của góc OAH. Giả sử éB > éC. Chứng minh éOAH = éB - éC. Cho éBAC = 600 và éOAH = 200. Tính: éB và éC của tam giác ABC. b) Diện tích hình viên phân giới hạn bởi dây BC và cung nhỏ BC theo R Lời giải: (HD) 1. AM là phân giác của éBAC => éBAM = éCAM => => M là trung điểm của cung BC => OM ^ BC; Theo giả thiết AH ^ BC => OM // AH => éHAM = éOMA ( so le). Mà éOMA = éOAM ( vì tam giác OAM cân tại O do có OM = OA = R) => éHAM = OAM => AM là tia phân giác của góc OAH. 2. Vẽ dây BD ^ OA => => éABD = éACB. Ta có éOAH = é DBC ( góc có cạnh tương ứng vuông góc cùng nhọn) => éOAH = éABC - éABD => éOAH = éABC - éACB hay éOAH = éB - éC. 3. a) Theo giả thiết éBAC = 600 => éB + éC = 1200 ; theo trên éB éC = éOAH => éB - éC = 200 . => b) Svp = SqBOC - SBOC = =
Tài liệu đính kèm:
 Cac dang toan thi vao lop 10.doc
Cac dang toan thi vao lop 10.doc





