Chuẩn kiến thức kỹ năng môn Toán lớp 5
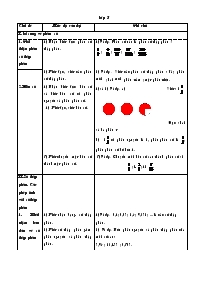
1) Nhận biết được phân số thập phân.
2) Biết đọc, viết các phân số thập phân.
1) Nhận biết được hỗn số và biết hỗn số có phần nguyên và phần phân số.
1) Biết đọc, viết hỗn số.
Bạn đang xem tài liệu "Chuẩn kiến thức kỹ năng môn Toán lớp 5", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
lớp 5 Chủ đề Mức độ cần đạt Ghi chú I. bổ sung về phân số 1. Giới thiệu phân số thập phân 1) Nhận biết được phân số thập phân. 1) Ví dụ. Phân số nào là phân số thập phân ? ; ; ; ; . 2) Biết đọc, viết các phân số thập phân. 2) Ví dụ. Viết các phân số thập phân : bảy phần mười ; hai mươi phần trăm ; một phần triệu. 2. Hỗn số 1) Nhận biết được hỗn số và biết hỗn số có phần nguyên và phần phân số. Biết đọc, viết hỗn số. 1) và 2) Ví dụ. a) Viết : 2 Đọc : hai và ba phần tư b) 2 có phần nguyên là 2, phần phân số là , phần phân số bé hơn 1. 3) Biết chuyển một hỗn số thành một phân số. 3) Ví dụ. Chuyển mỗi hỗn số sau thành phân số : 2 ; 4 ; 12. II. Số thập phân. Các phép tính với số thập phân 1. Khái niệm ban đầu về số thập phân 1) Biết nhận dạng số thập phân. 1) Ví dụ. 0,1; 0,07; 2,8; 9,572; ... là các số thập phân. 2) Biết số thập phân gồm phần nguyên và phần thập phân. 2) Ví dụ. Nêu phần nguyên và phần thập phân của mỗi số sau: 7,98 ; 25,477 ; 0,307. 3) Biết đọc và viết số thập phân. 3) Ví dụ. Đọc số thập phân; nêu phần nguyên, phần thập phân và và giá trị của mỗi chữ số trong số thập phân đó: 1,7 ; 2,35 ; 28,364 ; 900,90. 4) Biết viết số thập phân khi biết số đơn vị của mỗi hàng trong phần nguyên, phần thập phân. 4) Ví dụ. Viết số thập phân có : Năm mươi lăm đơn vị, năm phần mười, năm phần trăm, năm phần nghìn. 5) Biết số đo đại lượng có thể viết dưới dạng phân số thập phân thì viết được dưới dạng số thập phân và ngược lại. 2) Ví dụ. Viết số thập phân thích hợp vào chỗ chấm : 7dm = m = ... m ; 6g = kg = ... kg ; 8m 56cm = 8m = ... m. Ví dụ. Viết các số đo sau dưới dạng số đo bằng mét: a) 3,4 dm; b) 21,5 dm; c) 236 cm. 2. So sánh số thập phân 1) Biết cách so sánh hai số thập phân. (Thuộc quy tắc và biết vận dụng để so sánh các số thập phân). 1) Ví dụ. So sánh các số thập phân : a) 48,97 và 51,02 ; b) 96,4 và 96,38 ; c) 0,7 và 0,65 ; d) 28,3 và 28,300. 2) Biết sắp xếp một nhóm các số thập phân theo thứ tự từ bé đến lớn hoặc ngược lại. 2) Ví dụ. Xếp theo thứ tự từ bé đến lớn các số sau đây : 6,375 ; 9,01 ; 8,72 ; 6,735 ; 7,19. 3. Phép cộng và phép trừ các số thập phân 1) Biết cộng, trừ các số thập phân có đến ba chữ số ở phần thập phân, có nhớ không quá hai lượt. 1) Ví dụ. Đặt tính rồi tính : a) 25,46 + 38,24 ; b) 37,97 - 18,09 ; c) 39,205 + 8,677 ; d) 61,429 - 9,165. 2) Biết tính chất giao hoán, tính chất kết hợp của phép cộng các số thập phân và sử dụng trong thực hành tính. 2) Ví dụ. Tính bằng cách thuận tiện nhất : a) 4,68 + 6,03 + 3,97 b) 6,9 + 8,4 + 3,1 + 0,6. 3) Biết tính giá trị của các biểu thức có không quá ba dấu phép tính cộng, trừ, có hoặc không có dấu ngoặc. 3) Ví dụ. Tính : a) 5,27 + 14,35 + 9,25; b) 8,3 - 1,4 - 3,6; c) 18,64 - (6,24 + 10,5). 4) Biết tìm một thành phần chưa biết của phép cộng hoặc phép trừ. 4) Ví dụ. Tìm x: a) x + 4,32 = 8,67 ; b) 6,85 + x = 10,29; c) x - 3,64 = 5,86; d) 7,9 - x = 2,5. 4. Phép nhân các số thập phân 1) Biết thực hiện phép nhân có tích là số thập phân có không quá ba chữ số ở phần thập phân, trong một số trường hợp : - Nhân một số thập phân với một số tự nhiên có không quá hai chữ số, mỗi lượt nhân có nhớ không quá hai lần. - Nhân một số thập phân với một số thập phân, mỗi lượt nhân có nhớ không quá hai lần. 1) Ví dụ. Tính: a) 12,6 ´ 3 ; b) 6,8 ´ 15. 2) Biết nhân nhẩm một số thập phân với 10 ; 100 ; 1000 ; ...; hoặc với 0,1 ; 0,01 ; 0,001. 2) Ví dụ. Nhân nhẩm : a) 1,4 ´ 10 ; 2,1 ´ 100 ; 5,32 ´ 1000. b) 5579,8 ´ 0,1 ; 67,19 ´ 0,01 ; 7524,3 ´ 0,001. 3) Biết sử dụng một số tính chất của phép nhân trong thực hành tính giá trị của các biểu thức số. 3) Ví dụ. a) Tính bằng cách thuận tiện nhất : 7,38 ´ 1,25 ´ 80. b) Tính bằng hai cách : (6,75 + 3,25) ´ 4,2 ; 7,8 ´ 0,35 + 0,35 ´ 3,2. 5. Phép chia các số thập phân 1) Biết thực hiện phép chia, thương là số tự nhiên hoặc số thập phân có không quá ba chữ số ở phần thập phân, trong một số trường hợp : - Chia số thập phân cho số tự nhiên - Chia số tự nhiên cho số tự nhiên, thương tìm được là một số thập phân - Chia số tự nhiên cho số thập phân - Chia số thập phân cho số thập phân 1) Ví dụ. Tính : a) 67,2 : 7 135,5 : 25 b) 23 : 4 882 : 36 c) 9 : 4,5 2 : 12,5 d) 17,55 : 39 8,216 : 5,2 2) Biết chia nhẩm một số thập phân cho 10 ; 100 ; 1000 hoặc cho 0,1 ; 0,01 ; 0,001. 2) Ví dụ. Tính nhẩm : a) 43,2 : 10 2,07 : 10 2,23 : 100 b) 32 : 0,1 934 : 0,01 0,225 : 0,001 3) Biết tính giá trị các biểu thức số thập phân có đến ba dấu phép tính. 3) Ví dụ. Tính : a) 38,95 + 12,7 ´ 3,2 ; b) (128,4 - 73,2) : 2,4 - 18,32 ; c) 8,64 : (1,46 + 3,34) + 6,32. 4) Biết tìm một thành phần chưa biết của phép nhân hoặc phép chia với số thập phân. 4) Ví dụ. Tìm x : a) x ´ 1,8 = 72 c) 25 : x = 1,25 b) x : 2,5 = 4,02 6. Tỉ số phần trăm 1) Nhận biết được tỉ số phần trăm của hai đại lượng cùng loại. 1) Ví dụ. ở một trường tiểu học, cứ 100 học sinh thì có 30 học sinh giỏi. Tỉ số phần trăm giữa số học sinh giỏi và số học sinh của toàn trường là : 30%. 2) Biết đọc, viết tỉ số phần trăm. 2) Ví dụ. “Ba mươi phần trăm” viết là: 30%; đọc là : Ba mươi phần trăm. 3) Biết viết một số phân số thành tỉ số phần trăm và viết tỉ số phần trăm thành phân số. 3) Ví dụ. a) Viết thành tỉ số phần trăm : = = 50 : 100 = 50% b) Viết 75% dưới dạng phân số tối giản. 75% = = 4) Biết thực hiện phép cộng, phép trừ các tỉ số phần trăm; nhân tỉ số phần trăm với một số tự nhiên, chia tỉ số phần trăm cho một số tự nhiên khác 0. 4) Ví dụ. Tính: a) 27,5% + 38% ; b) 30% - 16% ; c) 14,2% ´ 4 ; d) 216% : 8. 5) Biết: - Tìm tỉ số phần trăm của hai số. - Tìm giá trị một tỉ số phần trăm của một số. - Tìm một số, biết giá trị một tỉ số phần trăm của số đó. 5) Ví dụ. a) Tìm tỉ số phần trăm của 303 và 600. b) Tìm 52,5% của 800. c) Tìm một số, biết 52,5% của số đó là 420. III. Yếu tố thống kê Biểu đồ hình quạt 1) Nhận biết về biểu đồ hình quạt và ý nghĩa thực tế của nó. 1) Ví dụ. Hình vẽ dưới đây là biểu đồ nói về kết quả học tập của lớp 5A. Khá 50% Giỏi 25% Trung bình 25% Nhìn vào biểu đồ ta biết, về kết quả học tập của lớp 5A có : 25% số học sinh giỏi ; 50% số học sinh khá ; 25% số học sinh trung bình. 2) Biết thu thập và xử lí một số thông tin đơn giản từ một biểu đồ hình quạt. 2) Ví dụ. Biểu đồ hình quạt dưới đây cho biết về tỉ số phần trăm các loại sách trong thư viện của một trường tiểu học: ...... .... Truyện thiếu nhi Sách giáo khoa và sách tham khảo Các loại sách khác 59,3% 30,5% 10% Hãy đọc tỉ số phần trăm của mỗi loại sách trên biểu đồ. Iv. Đại lượng và đo đại lượng 1. Bảng đơn vị đo độ dài (bổ sung) 1) Biết tên gọi, kí hiệu, mối quan hệ của các đơn vị đo độ dài trong bảng đơn vị đo độ dài. 1) Ví dụ. a) Viết theo mẫu: Lớn hơn mét Mét Bé hơn mét km hm dam m dm cm mm 1m =10dm =dam Trong bảng đơn vị đo độ dài : - Đơn vị lớn gấp bao nhiêu lần đơn vị bé hơn tiếp liền? - Đơn vị bé bằng một phần mấy đơn vị lớn hơn tiếp liền? 2) Biết chuyển đổi các đơn vị đo độ dài : a) Từ số đo có 1 tên đơn vị sang số đo có 1 tên đơn vị khác. b) Từ số đo có 2 tên đơn vị sang số đo có 1 tên đơn vị và ngược lại. 2) Ví dụ. Viết số thích hợp vào chỗ chấm: a) 135m = ... dm 8300cm = ... m 15km = ... m 150mm = ... cm b) 4km37m = ... m 354dm = ... m ... dm 8cm5mm = ... mm 3040m = ... km ... m 3) Biết thực hiện phép tính với các số đo độ dài và vận dụng trong giải quyết một số tình huống thực tế. 3) Ví dụ. Trên tuyến đường sắt Thống Nhất, quãng đường từ Hà Nội đến Đà Nẵng dài 791km. Quãng đường từ Đà Nẵng đến Thành phố Hồ Chí Minh dài hơn quãng đường trên 144km. Hỏi : a) Đường sắt từ Đà Nẵng đến Thành phố Hồ Chí Minh dài bao nhiêu ki-lô-mét ? b) Đường sắt từ Hà Nội đến Thành phố Hồ Chí Minh dài bao nhiêu ki-lô-mét ? 2. Bảng đơn vị đo khối lượng 1) Biết tên gọi, kí hiệu, mối quan hệ của các đơn vị đo khối lượng trong bảng đơn vị đo khối lượng. 1) Ví dụ. a) Viết theo mẫu: Lớn hơn ki-lô-gam Ki-lô-gam Bé hơn ki-lô-gam tấn tạ yến kg hg dag g 1kg =10hg = yến b) Trong bảng đơn vị đo khối lượng : - Đơn vị lớn gấp bao nhiêu lần đơn vị bé hơn tiếp liền? - Đơn vị bé bằng một phần mấy đơn vị lớn hơn tiếp liền? 2) Biết chuyển đổi các đơn vị đo khối lượng : a) Từ số đo có một tên đơn vị sang số đo có một tên đơn vị khác. b) Từ số đo có hai tên đơn vị sang số đo có một tên đơn vị và ngược lại. 2) Ví dụ. Viết số thích hợp vào chỗ chấm: a) 18 tạ = ... kg 4300kg = ... tạ 35 tấn = ... kg 65000kg = ... tấn b) 2kg326g = ... g 4008g = ... kg ... g 6kg3g = ... g 9350kg = ... tấn ... kg 3) Biết thực hiện phép tính với các số đo khối lượng và vận dụng trong giải quyết một số tình huống thực tế. 3) Ví dụ. Một cửa hàng trong ba ngày bán được 1 tấn đường. Ngày đầu bán được 300kg. Ngày thứ hai bán gấp 2 lần ngày đầu. Hỏi ngày thứ ba cửa hàng bán được bao nhiêu ki-lô-gam đường ? 3. Diện tích 1) Biết dam2, hm2, mm2 là những đơn vị đo diện tích ; ha là đơn vị đo diện tích ruộng đất. Biết đọc, viết các số đo diện tích theo những đơn vị đo đã học. 1) Ví dụ. a) Đọc : 29 mm2 ; 105dam2 ; 4925hm2. b) Viết số đo diện tích : Một trăm sáu mươi tám mi-li-mét vuông. Mười tám nghìn chín trăm đề-ca-met vuông. Ba nghìn sáu trăm hai mươi héc -tô-mét vuông. 2) Biết tên gọi, kí hiệu, mối quan hệ của các đơn vị đo diện tích trong bảng đơn vị đo diện tích. 2) Ví dụ. Viết số thích hợp vào chỗ chấm: a) 1km2 = ... hm2 1m2 = ... dm2 = dam2 b) 1km2 = ... m2 ; 1ha = ... m2 3) Biết chuyển đổi đơn vị đo diện tích : a) Từ số đo có một tên đơn vị sang số đo có một tên đơn vị khác. b) Từ số đo có hai tên đơn vị sang số đo có một tên đơn vị và ngược lại. 3) Ví dụ. Viết số thích hợp vào chỗ chấm : a) 8km2 = ... m2 20 000m2 = ... dam2 9m2 = ... cm2 b) 12m29dm2 = ... dm2 150cm2 = ... dm2 ... cm2 709mm2 = ... cm2 ... mm2 4) Biết thực hiện phép tính với các số đo diện tích. 4) Ví dụ. Tính: 896mm2 - 159mm2 ; 1270km2 ´ 8. 4. Thể tích 1) Biết cm3, dm3, m3 là những đơn vị đo thể tích. Biết đọc, viết các số đo thể tích theo những đơn vị đo đã học. 1) Ví dụ. a) Đọc các số đo: 76cm3 ; 85,08dm3 ; m3 ; 0,911m3 b) Viết các số đo thể tích: Bảy nghìn hai trăm mét khối ; Một phần tám đề-xi-mét khối ; Hai mươi tư phẩy năm xăng-ti-mét khối. 2) Biết mối quan hệ giữa m3 và dm3, dm3 và cm3, m3 và cm3. 2) Ví dụ. Viết số thích hợp vào chỗ chấm : 1dm3 = ... cm3 1m3 = ... dm3 1m3 = ... cm3 3) Biết chuyển đổi đơn vị đo thể tích trong trường hợp đơn giản. 3) Ví dụ 1. Viết số thích hợp vào chỗ chấm : a) 375dm3 = ... cm3 b) 2000cm3 = ... dm3 dm3 = ... cm3 5100cm3 = ... dm3 Ví dụ 2. Viết các số đo dưới dạng số đo bằng đề-xi-mét khối: 1cm3 ; 5,126m3 ; 13,8m3 ; m3 ; 0,22m3 5. Thời gian 1) Biết mối quan hệ giữa một số đơn vị đo thời gian thông dụng. 1) Ví dụ. Điền số thích hợp vào chỗ chấm : 1 thế kỉ = ... năm 1 tuần lễ có ... ngày 1 năm = ... tháng 1 ngày = ... giờ 1 năm (thường) có ... ngày 1 giờ = ... phút 1 năm (nhuận) có ... ngày 1 phút = ... giây 2) Biết đổi đơn vị đo thời gian. 2) Ví dụ. Viết số thích hợp vào chỗ chấm : a) 6 năm = ... tháng giờ = ... phút 3 năm rưỡi = ... tháng 0,5 ngày = ... giờ 2 giờ 15 phút = ... phút b) 60 giờ = ... ngày ... giờ 182 phút = ... giờ ... phút 75 giây = ... phút ... giây 3) Biết cách thực hiện phép cộng, phép trừ các số đo thời gian (có đến 2 tên đơn vị). 3) Ví dụ. Tính : a) 3 giờ 5 phút + 6 giờ 32 phút 12 phút 43 giây + 5 phút 37 giây b) 15 giờ 55 phút - 13 giờ 10 phút 3 phút 20 giây - 2 phút 45 giây 4) Biết cách thực hiện phép nhân, phép chia số đo thời gian (có đến 2 tên đơn vị) với (cho) một số tự nhiên khác 0. 4) Ví dụ. Tính : a) 3 giờ 12 phút ´ 3 b) 24 phút 12 giây : 4 12 phút 25 giây ´ 5 7 giờ 40 phút : 4 6. Vận tốc Bước đầu nhận biết được vận tốc của một chuyển động ; tên gọi, kí hiệu của một số đơn vị đo vận tốc (km/giờ, m/phút, m/ giây). Ví dụ. Một ô tô đi quãng đường dài 170km hết 4 giờ. Như vậy, trung bình mỗi giờ ô tô đi được : 170 : 4 = 42,5 (km). Ta nói vận tốc trung bình, hay nói tắt vận tốc của ô tô là 42,5km/ giờ (đọc là bốn mươi hai phẩy năm ki-lô-mét giờ). V. Yếu tố hình học 1. Hình tam giác 1) Nhận biết được các dạng hình tam giác : - Tam giác có ba góc nhọn. - Tam giác có một góc tù và hai góc nhọn. - Tam giác có một góc vuông và hai góc nhọn. 1) Ví dụ. 2) Biết cách tính diện tích của hình tam giác 2) Ví dụ. Tính diện tích hình tam giác có độ dài đáy là 8 cm và chiều cao là 6 cm. 2. Hình thang 1) Nhận biết được hình thang và một số đặc điểm của nó. 1) Ví dụ. Trong các hình sau, hình nào là hình thang ? 2) Biết cách tính diện tích của hình thang. 2) Ví dụ. Tính diện tích hình thang biết : độ dài đáy lớn là 12cm, độ dài đáy nhỏ là 8cm và chiều cao là 5cm. 3. Hình tròn Biết cách tính chu vi và diện tích của hình tròn. Ví dụ 1. Tính chu vi hình tròn : a) Có đường kính d = 0,6cm; b) Có bán kính r = 1,2m. Ví dụ 2. Tính diện tích hình tròn : a) Có bán kính r = 5cm; b) Có đường kính d = 12cm. 4. Hình hộp chữ nhật. Hình lập phương 1) Nhận biết được hình hộp chữ nhật và hình lập phương và một số đặc điểm của nó. 1) Ví dụ. Điền số thích hợp vào chỗ chấm : Số mặt Số cạnh Số đỉnh Hình hộp chữ nhật Hình lập phương 2) Biết cách tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật và hình lập phương. 2) Ví dụ1. Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật có chiều dài 5dm, chiều rộng 4dm và chiều cao 3dm. Ví dụ 2. Người ta làm một cái hộp không có nắp bằng bìa cứng dạng hình lập phương có cạnh 2,5dm. Tính diện tích bìa phải dùng để làm hộp (không tính mép dán). 3) Biết cách tính thể tích hình hộp chữ nhật và hình lập phương. 3) Ví dụ 1. Tính thể tích hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm và chiều cao 4cm. Ví dụ 2. Tính thể tích hình lập phương có cạnh là 3cm. 5. Hình trụ 1) Nhận biết được hình trụ. 1) Ví dụ. Trong các hình dưới đây, hình nào là hình trụ ? 6. Hình cầu Nhận biết được hình cầu. Ví dụ. Trong các hình dưới đây, hình nào là hình cầu ? III. Giải bài toán có lời văn Biết giải và trình bài giải các bài toán có đến bốn bước tính, trong đó có các bài toán về: 1) “Quan hệ tỉ lệ”. Ví dụ1. Trong 1 giờ, 2 công nhân đào được 7m rãnh để đặt ống nước. Hỏi với mức đào như vậy, trong 1 giờ, 6 công nhân đào được bao nhiêu mét rãnh ? Ví dụ 2. Muốn đắp xong một nền nhà trong 4 ngày, cần có 6 người. Hỏi muốn đắp xong nền nhà đó trong 3 ngày thì cần có bao nhiêu người ? (mức làm như nhau). 2) Tỉ số phần trăm Ví dụ 1. Một trường học có 600 học sinh, trong đó có 303 học sinh nữ. Hỏi số học sinh nữ chiếm bao nhiêu phần trăm số học sinh toàn trường ? Ví dụ 2. Lãi suất tiết kiệm là 0,5% một tháng. Một người gửi tiết kiệm 5 000 000 đồng. Tính số tiền lãi tiết kiệm sau một tháng. Ví dụ 3. Số học sinh nữ của một trường là 420 em và chiếm 52,5% số học sinh toàn trường. Hỏi trường đó có bao nhiêu học sinh ? 3) Chuyển động đều Ví dụ 1. Một máy bay bay được 1800km trong 2 giờ 15 phút. Tính vận tốc của máy bay. Ví dụ 2. Một người đi xe đạp trong 2 giờ 30 phút với vận tốc 12,6km/giờ. Tính quãng đường đi được của người đó. Ví dụ 3. Một ca nô đi với vận tốc 18km/giờ trên quãng đường sông dài 42km. Tính thời gian đi của ca nô trên quãng đường đó. Ví dụ 4: Hai thành phố A và B cách nhau 150km. Một xe máy đi từ thành phố A đến thành phố B với vận tốc 35km/giờ, cùng lúc đó một ô tô đi ngược chiều với xe máy từ thành phố B đến thành phố A với vận tốc 65km/giờ. Hỏi sau bao lâu ô tô và xe máy gặp nhau ? Ví dụ 5: Một người đi xe đạp khởi hành từ A đến B với vận tốc 12km/giờ. Sau 3 giờ một xe máy cũng đi từ A đến B với vận tốc 36km/giờ. Hỏi từ lúc xe máy bắt đầu đi thì sau bao lâu xe máy đuổi kịp xe đạp ? 4) Nội dung hình học Ví dụ 1. Một thửa ruộng hình thang có đáy lớn 120m, đáy bé bằng 2/3 đáy lớn, chiều cao kém đáy bé 5m. Trung bình 100m2 thu hoạch được 64,5kg thóc. Tính số ki-lô-gam thóc thu hoạch trên thửa ruộng đó. 22 cm Ví dụ 2. Người ta xếp các viên gạch hình hộp chữ nhật tạo thành một hình lập phương cạnh 22cm. a) Tính kích thước của mỗi viên gạch. b) Tính diện tích toàn phần của hình lập phương.
Tài liệu đính kèm:
 Chuan KT Ky nang Toan lop 5.doc
Chuan KT Ky nang Toan lop 5.doc





