Toán 5 - Tổng hợp các kiến thức lớp 5 cần nhớ

TỔNG HỢP CÁC KIẾN THỨC LỚP 5 CẦN NHỚ
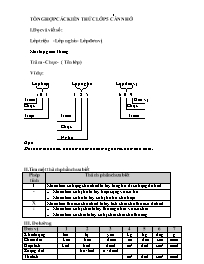
I.Đọc và viết số:
Lớp triệu - Lớp nghìn - Lớp đơn vị
Mỗi lớp gồm 3 hàng
Trăm - Chục - ( Tên lớp)
Ví dụ:
 Lớp triệu Lớp nghìn Lớp đơn vị
 1 0 3 3 2 5 6 0 9 
Trăm Đơn vị
Chục Chục
Triệu Trăm Trăm 
 Chục 
 Nghìn
Đọc:
Một trăm lẻ ba triệu ba trăm hai mươi lăm nghìn sáu trăm linh chín.	
II.Tìm một thành phần chưa biết
Phép tính
Thành phần chưa biết
+
Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết
-
Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ
Muốn tìm số trừ ta lấy số bị trừ trừ cho hiệu 
X
Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết
:
Muốn tìm số bị chia ta lấy thương nhân với số chia
Muốn tìm số chia ta lấy số bị chia chia cho thương
III. Đo lường
Đơn vị
1
2
3
4
5
6
7
Khối lượng
tấn
tạ
yến
kg
hg
dag
g
Chiều dài
km
hm
dam
m
dm
cm
mm
Diện tích
km2
hm2
dam2
m2
dm2
cm2
mm2
Ruộng đất
ha=hm2
a =dam2
Thể tích
m3
dm3
cm3
mm3
Dung tích
lít
Thời gian 
thế kỷ
100 năm
năm
365/366 ngày
12 tháng
tháng
30/31ngày
tuần
7 ngày
ngày
24 giờ
giờ
60 phút
phút
60giây
Ghi chú:
Hai đơn vị đo khối lượng liền nhau hơn kém nhau 10 lần
Hai đơn vị đo chiều dài liền nhau hơn kém nhau 10 lần
Hai đơn vị đo diện tích liền nhau hơn kém nhau 100 lần
 1 ha = 1 hm2 = 10 000 m2
Hai đơn vị thể tích liền nhau hơn kém nhau 1 000 lần
Một năm thường có 365 ngày riêng năm nhuận ( chia hết cho 4 ) có 366 ngày
1 tháng thường có 31 ngày riêng tháng 2 có 28 ngày ( năm nhuận 29 ngày), tháng 4,6, 9,11 có 30 ngày
IV. Hình học
Hình
Chu vi
Diện tích
Công thức mở rộng
Hình vuông
C= 4 x a
C: chu vi
a : cạnh
S = a x a
S: diện tích 
a = C : 4
Chữ nhật
C= (d+ r) x 2
d : chiều dài
r : chiều rộng 
S = d x r
d + r = C : 2
d = S : r
r = S : d
Tam giác
S = 
a : cạnh đáy
h : đường cao
a = 
h =
Hình thang
S = 
a : đáy lớn
b: đáy nhỏ
h: đường cao
a + b = 
h = 
Hình tròn
2 x r = d
d : đường kính
C = 2 x r x 3,14
r = bán kính
C = chu vi
S= r x r x 3, 14
S = diện tích
d = 2 x r 
d = C : 3, 14 
Hình
Diện tích 
Thể tích
Công thức mở rộng
Hình hộp chữ nhật 
Sxq = Cd x h
Stp = Sxq + 2 x Sd
Cd = Chu vi đáy
 h = chiều cao
Sd = diện tích mặt đáy 
V = Sd x h 
V : thể tích
Sd = V : h
 h = V : Sd
 Cd = Sxq : h
 h = Sxq : Cd 
Hình khối lập phương
Sxq = 4 x a x a 
Stp = 6 xa x a
Sxq : diện tích xung quanh
Stp :diện tích toàn phần 
a : cạnh 
V = a x a x a
V : thể tích
= 
Hình trụ
Sxq = Cd x h
Stp = Sxq + 2 x Sd
Cd : chu vi đáy 
Cd = 2 x r x 3,14 
V = Sd x h
Sd : diện tích đáy
Sd = r x r x 3, 14
h : chiều cao 
Sd = V : h
V. Các dạng toán thường gặp 
1.Tìm số trung bình cộng
Muốn tìm số trung bình cộng của nhiều số , ta lấy tổng của các số hạng chia cho số các số hạng.
Trung bình cộng = Tổng các số hạng : Số các số hạng
2.Tìm hai số khi biết tổng và hiệu :
Cách 1 :
Cách 2:
Số nhỏ = ( Tổng - hiệu ) : 2
Số lớn = Tổng - số nhỏ
Hoặc :
Số lớn = Số nhỏ + hiệu
Số lớn = ( Tổng + hiệu ) : 2
Số nhỏ = Số lớn - hiệu
Hoặc:
Số nhỏ = Tổng - Số lớn
3.Tìm hai số khi biết tổng và tỉ
Bốn bước:
Tìm tổng số phần bằng nhau
Tìm giá trị của một phần: Lấy tổng hai số chia cho số phần bằng nhau
Tìm số thứ nhất : Lấy giá trị một phần nhân với số phần của số thứ nhất
Tìm số thứ hai : Lấy tổng hai số trừ đi số thứ nhất (hoặc lấy giá trị của một phần nhân với số phần của số thứ hai)
4.Tìm hai số khi biết hiệu và tỷ
Bốn bước:
Tìm hiệu số phần bằng nhau
Tìm giá trị của một phần: Lấy hiệu của hai số chia cho hiệu số phần bằng nhau
Tìm số thứ nhất : Lấy giá trị một phần nhân với số phần của số thứ nhất
Tìm số thứ hai : Lấy giá trị của một phần nhân với số phần của số thứ hai.
5. Đại lượng tỷ lệ thuận:
Định nghĩa : Hai đại lượng gọi là tỷ lệ thuận với nhau khi đại lượng này tăng ( hay giảm ) bao nhiêu lần thì đại lượng kia cũng tăng ( hay giảm) bấy nhiêu lần.
Cách giải:
Xác định các đại lượng tỷ lệ thuận với nhau
Dùng phương pháp rút về đơn vị ( hoặc phương pháp dùng tỉ số ) để giải bài toán. 
Ví dụ :
Một người đi bộ trong ba giờ đi được 18 km. Hỏi trong 6 giờ người ấy đi được mấy km ?
Cách 1: Rút về đơn vị
Tóm tắt : 3 giờ .18 km
 6 giờ .. ? km
Nhận xét: Thời gian và quãng đường là hai đại lượng tỉ lệ thuận với nhau.
 Giải :
 Một giờ người đi bộ đi được :
 18 : 3 = 6 (km/ giờ )
 Trong 6 giờ người đó đi được :
 6 x 6 = 36 ( km)
 Đáp số : 36 km
Cách 2:Phương pháp dùng tỉ số
Tóm tắt : 3 giờ .18 km
 6 giờ .. ? km
 Giải
3 giờ so với 6 giờ thời gian tăng lên:
 6 : 3 = 2 ( lần )
Quãng đường người ấy đi được trong 6 giờ là :
 18 x 2 = 36 ( km)
 Đáp số : 36 km
6. Đại lượng tỷ lệ nghịch :
Định nghĩa : Hai đại lượng gọi là tỷ lệ nghịch với nhau khi đại lượng này tăng ( hay giảm ) bao nhiêu lần thì đại lượng kia giảm ( hay tăng) bấy nhiêu lần.
Cách giải:
Xác định đại lượng nào tỷ lệ nghịch với đại lượng nào
Dùng phương pháp rút về đơn vị ( hoặc phương pháp dùng tỉ số ) để giải bài toán. 
Ví dụ 1:
18 người làm xong một con đường trong 5 ngày . Hỏi với mức làm như vậy , 6 người sẽ làm xong con đường ấy trong bao nhiêu ngày ?( Giả sử sức làm mỗi người như nhau )
Cách 1: Rút về đơn vị
Tóm tắt
 18 người ...................5 ngày
 6 người .....................? ngày
Nhận xét : Số người và số ngày làm xong quãng đường là hai đại lượng tỷ lệ nghịch với nhau .
 Giải
Số ngày 1 người làm xong đoạn đường trên là :
 18 x 5 = 90 (ngày)
Số ngày 6 người làm xong đoạn đường trên là :
 90 : 6 = 15 ( ngày )
 Đáp số : 15 ngày
Cách 2 : Dùng tỷ số 
 Giải 
18 người so với 6 người thì số người giảm đi :
 18 : 6 = 3 ( lần )
Số ngày 6 người làm xong đoạn đường là :
 5 x 3 = 15 ( ngày )
 Đáp số 15 ngày 
VI. Phân số : Những điều cần ghi nhớ 
Phân số thập phân là các phân số có mẫu có mẫu số là 10 , 100 , 1 000....
Mọi số tự nhiên có thể viết dưới dạng phân số có mẫu số là 1.
Ví dụ : 6 = ; 15 = 
 3.Cộng hai phân số 
a. Nếu cùng mẫu số :Cộng hai tử số với nhau và giữ nguyên mẫu số.
b. Hai phân số khác mẫu số :Quy đồng mẫu số hai phân số , sau đó cộng hai phân số đã được quy đồng.
 4.Trừ hai phân số 
a. Nếu cùng mẫu số : Trừ hai tử số với nhau và giữ nguyên mẫu số.
b. Hai phân số khác mẫu số :Quy đồng mẫu số hai phân số , sau đó trừ hai phân số đã được quy đồng.
 5. Nhân hai phân số
 Lấy tử số nhân với tử số , mẫu số nhân với mẫu số .
 6. Chia hai phân số 
Lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược .
 7.Rút gọn phân số :
Phân tích tử và mẫu rồi rút gọn
 Ví dụ : === ; ==
Xem tử và mẫu cùng chia hết cho số nào >1 , rút gọn cho đến hết .
Lưu ý những số chia hết cho 7 và 17 .
 8.Quy đồng mẫu số: 
(Lưu ý nên tối giản trước khi quy đồng , trừ những trường hợp đặc biệt* )
Ví dụ 1 :
QĐ ; Ta có = và = nên QĐ ; ta được và 
Ví dụ 2 :
QĐ và vì 12: 6 = 2 ta có = nên QĐ và ta được và 
Ví dụ 3 : *
QĐ ; ta có = nên QĐ , ta được và ( không rút gọn )
QĐ ta có ; ta có nên QĐ ta được = và = 
So sánh phân số:
Để so sánh ta có thể sử dụng các cách:
Quy đồng mẫu :
Xếp thứ tự các phân số sau từ bé đến lớn : ; ; 
Ta có = ; = ; nên << 
Quy đồng tử :
Xếp thứ tự các phân số sau từ bé đến lớn : ;;
Ta có = = nên < < 
Dùng số làm trung gian :
Xếp thứ tự các phân số sau từ bé đến lớn : ;; ;;
Ta có ; ; 2 ; = = nên <<<<
VII. Số thập phân : Những điều cần nhớ
1.Mỗi số thập phân gồm hai phần , phần nguyên và phần thập phân , giữa hai phần này có dấu phẩy.
Những chữ số bên trái dấu phẩy là phần nguyên
Những chữ số bên phải dấu phẩy là phần thập phân
2. Số thập phân bằng nhau
Nếu ta viết thêm chữ số 0 vào bên phải phần thập phân của một số thập phân thì được một số thập phân bằng nó
Nếu một số thập phân có chữ số 0 tận cùng bên phải phần thập phân , thì khi bỏ chữ số 0 đó ta được một số thập phân bằng nó.
3.So sánh hai số thập phân 
So sánh phần nguyên của hai số đó như so sánh hai số tự nhiên . Số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn
Nếu phần nguyên bằng nhau thì so sánh phần thập phân , lần lượt từ hàng phần mười , hàng phần trăm , hàng phần nghìn ... cho đến khi cùng một hàng nào đó , số thập phân có hàng tương ứng lớn hơn thì số đó lớn hơn.
4.Cộng hai số thập phân :
Ta viết số hạng này dưới số hạng kia sao cho các chữ số cùng hàng thẳng cột với nhau, các dấu phẩy đặt thẳng cột với nhau.
Cộng như cộng các số tự nhiên
Đặt dấu phẩy ở tổng thẳng cột với các dấu phẩy của các số hạng.
5. Trừ một số thập phân với một số thập phân:
Ta viết số trừ dưới số bị trừ sao cho các chữ số cùng hàng đặt thẳng cột với nhau , các dấu phẩy thẳng cột với nhau.
Trừ như trừ các số tự nhiên
Đặt dấu phẩy ở hiệu thẳng cột với các dấu phẩy của số bị trừ và số trừ.
6.Phép nhân 
a. Nhân một số thập phân với một số tự nhiên
Ta thực hiện phép nhân như đối với số tự nhiên
Đếm xem trong phần thập phân có bao nhiêu chữ số , dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái 
b.Nhân số thập phân với 10 , 100 ...
Ta chỉ việc chuyển dấu phẩy của số thập phân sang bên phải một , hai ...chữ số.
c.Nhân một số thập phân với một số thập phân:
Ta thực hiện phép nhân như đối với số tự nhiên
Đếm xem trong phần thập phân của hai thừa số có bao nhiêu chữ số, dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.
7. Phép chia:
a. Chia một số thập phân cho một số tự nhiên
Ta chia phần nguyên của số bị chia cho số chia
Đánh dấu phẩy vào thương đã tìm được trước khi lấy chữ số đầu tiên của phần thập phân ở số bị chia để đưa vào phép chia
Tiếp tục phép chia với từng chữ số của phần thập phân ở số bị chia.
b.Chia một số thập phân cho 10 , 100 , 1 000....
Ta chỉ việc chuyển dấu phẩy của số thập phân sang bên trái một , hai , ba ....chữ số 
c.Chia một số tự nhiên cho một số tự nhiên thương tìm được là một số thập phân
Khi chia một số tự nhiên cho một số tự nhiên còn dư, ta có thể tiếp tục thực hiện phép chia sau:
Đánh dấu phẩy vào bên phải của thương.
Thêm vào bên phải số dư một số 0 rồi chia tiếp tục.
Nếu số dư còn nữa, ta lại thêm vào bên phải số dư mới một chữ số 0 rồi tiếp tục chia ....
d.Chia một số tự nhiên cho một số thập phân
Ta đếm xem có bao nhiêu chữ số ở phần thập phân của số chia thì thêm vào bên phải số bị chia bấy nhiêu chữ số 0.
Bỏ dấu phẩy ở số chia và thực hiện phép chia như như đối với các số tự nhiên.
e.Chia số thập phân cho số thập phân
Ta đếm xem có bao nhiêu chữ số ở phần thập phân của số chia thì chuyển dấu phẩy ở số bị chia sang bên phải bấy nhiêu chữ số.
Bỏ dấu phẩy ở số chia rồi thực hiện phép chia như đối với các số tự nhiên.
8.Học thuộc lòng quy tắc tính nhẩm
a x 0,25 = a : 4
a : 0,25 = a x 4
a x 0,5 = a : 2
a : 0,5 = a x 2
a x 25 = a x 100 : 4
Muốn nhân một số thập phân với 0,1 ; 0,01 ; 0 ; ta dời dấu phẩy của số đó sang trái 1 ; 2; 3...chữ số.
Muốn chia một số thập phân cho 0,1 ; 0,01 ; 0,001 ...ta dời dấu phẩy của số đó sang phải là 1 ; 2; 3; .....chữ số.
VIII.Tỷ số phần trăm
1. Muốn tính tỷ số phần trăm của hai số:
Tìm thương của hai số đó rồi viết thương dưới dạng số thập phân
Nhân thương đó với 100 rồi viết thêm ký hiệu % vào bên phải tích tích vừa tìm được.
2. Muốn tìm 52, 5 % của 800 :
Lấy 800 chia cho 100 tìm giá trị 1 %
Lấy số tìm được x 52 , 5 tìm giá trị của 52,5%( Giống như phân số của một số ) 
3. Tìm một số biết 52,5 % của số đó là 420 ta làm như sau :
Lấy 420 chia cho 52, 5 để tìm 1% của số đó 
Lấy giá trị vừa tìm được x 100 để tìm nguyên số
IX.Chuyển động đều:
Công thức :
V = S : t
S = V x t
t = S : V
Trong đó :
V : Vận tốc
S : quãng đường
t : thời gian
a. Hai chuyển động cùng chiều:
Muốn tính thời gian từ lúc bắt đầu đi đến khi đuổi kịp nhau , ta lấy khoảng cách giữa hai vật chia cho hiệu vận tốc của chúng :
A B C 
 V1 V2
Thời gian để hai chuyển động gặp nhau là : t = (với V1 > V2 )
b. Hai chuyển động ngược chiều :
Muốn tính thời gian từ lúc khởi hành đến khi gặp nhau , ta lấy quãng đường giữa hai chuyển động chia cho tổng vận tốc của chúng : 
A C B 
V1 V2
Thời gian để hai chuyển động gặp nhau là : t = 
Lưu ý :
Để thực hiện các phép tính trên các số đo thời gian cần chuyển về cùng một đại lượng.
c.Chuyển động trên sông :
a. Xuôi dòng : 
Vận tốc chuyển động bằng vận tốc thực cộng vận tốc dòng nước.
b.Ngược dòng:
Vận tốc chuyển động bằng vận tốc thực trừ vận tốc dòng nước.
X Các bài toán về dãy số cách đều :
a.Số số hạng của một dãy số cách đều = (số lớn nhất - số bé nhất ): khoảng cách + 1
 (số lớn nhất + số bé nhất ) x số các số hạng
b.Tổng các số hạng của dãy số cách đều = 
 2
c. Một số hạng của dãy số cách đều:
Số hạng thứ n = số đầu + (n – 1 )x khoảng cách (Đối với dãy số tăng)
Số hạng thứ n = số đầu - (n – 1 )x khoảng cách (Đối với dãy số giảm)